Semesteroppgave i musikkvitenskap grunnfag, Universitet i Oslo, levert 1. juni, 1999.
Forord
En oppgave i musikkteknologi innbefatter delområder fra både matematikk, informatikk, fysikk og musikk. Nettopp denne allsidigheten var det som lokket meg til å skrive en oppgave innen dette feltet. Med universitetsbakgrunn fra alle fagområdene synes jeg det har vært spennende å endelig kunne kombinere erfaringene fra de forskjellige feltene for å skrive en oppgave.
Jeg tok tidlig kontakt med NOTAM og fikk full anledning til å bruke utstyr og programvare fra deres maskinpark. I tillegg ble jeg veiledet i hvordan jeg skulle bruke de forskjellige programmene og lydutstyret. Dette har vært uvurderlig i mitt arbeide, som i all hovedsak har bestått av å lære å bruke og forstå mange forskjellige programmer for signalprosessering og lydsyntese både for PC, Mac og Unix. Mye tid har derfor gått med til å lese bakgrunnsinformasjon og manualer, men dette har vært en spennende læringsprosess. Jeg har lagt vekk på å ikke bare skrive en oppgave, men å stikke hodet inn i et fagfelt som er i drivende utvikling. Selv med kun to ukers døgnkontinuerlig arbeide, føler jeg at jeg har fått en viss oversikt over fagområdet musikkteknologi og kjennskap til endel av utstyret og programvaren som blir benyttet.
For å generere egne lyder har jeg satt meg inn i lydprogrammeringsspråket Csound som i lang tid har vært selve hjørnestenen i digital lydbehandling. Ved å kunne teste ut de forskjellige teoriene i praksis har jeg også forstått mer av de forskjellige elementenes oppbygning.
Denne oppgaven er skrevet i typesettingsprogrammet LaTeX. Dette var fordi jeg ønsket å teste ut den omgivelsen som de fleste universitetsfolk (ihvertfall på MatNat) skriver sine oppgaver og avhandlinger i.
For å klargjøre de forskjellige punktene og som illustrasjoner har jeg lagt ved en CD-plate. Gjennom hele oppgaven henvises det til aktuelle spor på CD-platen. En oversikt over sporene på CDen står i appendixet.
Jeg vil takke min veileder Rolf-Inge Godøy på IMT og Bjarne Kvinnsland og Øyvind Hammer på NOTAM for all hjelp.
Innledning
Digital signalprosessering og digitale instrumenter har blitt en viktig del av dagens musikkliv. I løpet av noen få år har disse områdene økt fra å være en kuriositet for spesielt interesserte til å bli ledende innen studiovirksomhet og på instrumentfronten. Jeg har selv blitt imponert over anslag og tone i mitt nye digitalpiano Roland RD-600, og har sett en rekke spennende redigeringsmuligheter i moderne dataprogrammer. Jeg ønsket imidlertid å lære mer om hva som egentlig skjer når jeg spiller på en tangent på pianoet mitt, eller prosesserer en lyd på datamaskinen. Særlig interessant er det å studere noen av områdene som vanskeliggjør et godt resultat, og se hvilke begrensninger og muligheter som ligger i dette.
I begynnelsen av oppgaven gjennomgår jeg en del viktige fysiske elementer. Dette er på ingen måte utfyllende nok, men det er heller ikke rom for nærmere utdypinger i en slik oppgave. Stort sett har jeg forsøkt å forklare alle begreper slik at alle skal kunne forstå det, men i kapitlet om Fourier-omvending forutsettes det en viss bakgrunnskunnskap i matematikk for å forstå formlene. Jeg ønsket allikevel å ta dem med fordi de er såpass sentrale i moderne lydbehandling.
For bedre å forstå hvordan lydsyntese egentlig fungerer forsøkte jeg å programmere en pianotone i Csound. I dag bruker imidlertid de fleste digitalpianoer lydsamplinger, og jeg har også brukt Samplecell for å lage mitt eget samplepiano.
Men hva er egentlig meningen med å forsøke å utvikle et perfekt digitalt instrument? Hvorfor skal man forsøke å etterligne et allerede perfekt akustisk piano? Meningen med å produsere og stadig utvikle bedre digitale instrumenter er ikke for å erstatte vanlige akustiske instrumenter, men er ment som et nyttig supplement.
Når man nevner ordet digitalpiano er det mange mennesker som øyeblikkelig stadfester at et digitalpiano overhodet ikke kan måle seg med akustiske instrumenter. Som en liten test på hvor dyktige folk egentlig er til å høre forskjell på dette, laget jeg en liten blindtest og intervjuet tilfeldige mennesker.
Gjennom oppgaven henvises det ofte til notenavn. Følgende betegnelser benyttes, med start fra de dypeste tonene: 1C, C, c, c1, c2, c3, c4, c5 (Benestad 1985:21).
Lyd
Lydbølger er kompresjoner i luften på samme måte som for eksempel lys. Disse kompresjonene registreres av trommehinnen i menneskeøret og forplanter seg videre til hjernen slik at vi oppfatter signalet som lyd. Lydbølger kan spres i alle medier, men hastigheten varierer avhengig av mediet. I luft med 20 grader celsius beveger lyden seg med 343 meter per sekund. I andre materialer, som for eksempel jern, beveger lyden seg med opptil flere kilometer per sekund, mens hastigheten i vann er svært liten. Forskjellige instrumentlyder får gjerne noe av sin spesielle klang på grunn av hastigheten i materialet som instrumentet er laget av.
Men hva er egentlig en bølge? Matematisk kan den settes opp ved hjelp av likningen

hvor lille a betyr at det er et analogt signal, Λ er amplituden, f er frekvensen i hertz, t er tiden i sekunder og δ er fasen (Proakis 1992:13). En helt ren lydbølge ser altså ut som en sinusfunksjon som i figur 1.

Figure 1: En ren sinustone
Fra en lydkilde spres signalet i alle retninger akkurat slik som bølgene fra en sten som kastes i vannet. Men ettersom bølgene beveger seg vekk fra kilden, er det viktig å huske på at lydstyrken blir mindre. Lydstyrken avtar faktisk med ganske nøyaktig kvadratet av avstanden til lydkilden.
For å kunne forstå videre arbeid med digitalisering av lyd, er det viktig at man kjenner til begrepene amplitude, frekvens, klangfarve, dynamikk og beats
Amplitude
Amplituden er det vertikale utslaget i en funksjon (figur 1), og angir lydens styrke målt i desiBel (forkortes dB). Dette er en logartimisk enhet, slik at hvis man for eksempel tredobler amplituden vil man nidoble lydstyrken. Derfor er det viktig at “vi ikke kan øke amplituden lineært og så regne med at vi får et naturlig crescendo. Vi må istedet bruke en eller annen eksponensiell funksjon” (Hammer 1997: 21).
Mennesket er istand til å skille to lyder med 1 dB forskjell og kan høre lyd opp til 120 dB før det gjør vondt. Når vi vet at det dynamiske området er definert som maksimumgrense over skillegrense, gir dette en verdi på 120 dB for menneskets øre. Vanlig lydutstyr har gjerne et dynamisk område på rundt 100 dB, og det er viktig å ta hensyn til dette når man arbeider med studioutstyr.
Frekvens
Perioden til en bølge er gitt ved tiden, målt i sekunder, fra en bølgetopp til den neste. Frekvens er definert som den inverse av perioden, og er et mål på hvor ofte svingningen gjentas i løpet av et sekund. Frekvens måles i hertz (Hz), og vi oppfatter den som tonens høyde. Enstrøken a har siden 1953 (Benestad 1985:60) vært definert med en frekvens på 440 Hz, det vil si at strengen beveger seg med 440 svingninger per sekund. På samme måte som for amplituden, er også frekvensen en logaritmisk enhet. Dette passer med at vårt notesystem er bygget opp slik at hvis man dobler frekvensen til en tone, hører vi dette som et oktavsprang opp. Tonen a2 har derfor en frekvens på 880 Hz, mens a har en frekvens på 220 Hz. Dette er svært nyttig når man arbeider med synthesiezere ettersom man enkelt kan bestemme frekvensen til enhver tone, kun ved å ta utgangspunkt i en annen tones frekvens og multiplisere denne med forholdet mellom de to tonene.
Klangfarve
Klangfarven er den unike formen til en lyd som gjør at man kan skille den fra en annen. En helt ren tone har gjerne form som en sinusfunksjon og er jevnt periodisk i tidsspekteret. Alle vanlige akustiske instrumenter har imidlertid en mye mer avansert oppbygging. Når for eksempel en pianostreng klinger, er lyden sammensatt av en rekke forskjellige sinus-funksjoner.
Matematikeren Fourier viste hvordan “enhver periodisk funksjon kan konstrueres ved å summere et antall sinus- og cosinus-funksjoner, hver med en frekvens som er et heltallsmultiplum av frekvensen til den periodiske funksjonen” (Hammer 1997:18). I tillegg adderes flere deltoner som kommer fra for eksempel resonans i instrumentet. Totalt skaper alle disse bølgene den kompliserte bølgefunksjonen som mennesket oppfatter. En forandring i en av parameterene vil altså være med på å endre klangfarven, og det vil mennesket kunne registrere og memorere for senere gjenkjennelse. Det er derfor vi klarer å skille mellom lyden fra for eksempel et piano og en obo.
Dynamikk
Vi har sett litt på hvordan en tone er bygget opp, men har ikke sett på hvordan den utvikler seg over tid. Når man hører på en pianotone (spor 4), merker man at den endrer seg hele tiden. Både lydstyrken, frekvensen og klangfarven forandres gjennom forløpet og er med på å skape det endelige inntrykket.
For det første endres amplituden kontinuerlig. Når en pianotone slås an, inntreffer nesten umiddelbart et maks-nivå i lydstyrken som kalles attack. Deretter følger en decay når amplituden langsomt dør ut. I tillegg må man ta hensyn til hvordan lyden skal være når man holder en pedal inne (sustain) og når man slipper pedalen (release). For noen år siden var det vanlig at de fleste synthesizere kun tok hensyn til disse fire punktene, populært kalt ADSR (Attack-Decay-Sustain-Release) (Hammer 1997:25). En slik beskrivelse av tonen over tid kalles gjerne for tenvelope og visualisert i tidsspekteret kan dette se ut som i figur 2. Her er de fire punktene tegnet lineært med knekkpunkter på grafen. For å gi en mer realistisk overgang mellom de forskjellige delene tegnes en slik envelope vanligvis mer buet og gjerne med en eksponensiell decay. Det viste seg imidlertid fort at bare fire punkter ble for lite for å beskrive en tone særlig realistisk, så de fleste moderne synthesizere bruker gjerne mange flere knekkpunkter og har en mengde med forskjellige innstillinger for å endre lydparametrene.

Figure 2: En ADSR (Attack-Decay-Sustain-Release) Envelope
Dynamikk i frekvensen er også svært viktig. Hvis man skal spille forskjellige toner kan man da enkelt minske eller øke hastigheten, med en endring i tonehøyde som resultat. Det kan også være aktuelt å endre frekvensen på en enkelt tone for å lage for eksempel glissando eller vibrato på enkelttoner (Hammer 1997:26).
For å skape en naturtro lyd må også klangfarven varieres. En pianotone har for eksempel en helt annen klang i selve anslaget enn når den er like ved å dø ut. å endre på denne parameteren krever mange beregninger og har tidligere vært begrenset av maskinvaren. Med dagens raske maskiner har man i større grad mulighet til å endre klangfarven kontinuerlig.
Beats
Hvis to toner med nærliggende frekvenser spilles samtidig vil man kun høre en tone med en frekvens som ligger midt mellom de to opprinnelige tonene. Denne tonen vil pulsere med en frekvens som er lik differansen mellom de to opprinnelige tonene. Dette kalles beats og antallet beats per sekund er lik forskjellen mellom de to frekvensene. La oss for eksempel spille en tone med frekvens 440 Hz og en annen med 445 Hz samtidig. Da vil vi høre en tone med frekvens 442,5 Hz som pulserer med en frekvens på 5 Hz. Denne effekten brukes blant annet når man stemmer en gitar eller et piano, for man kan da justere strengene til man ikke lenger hører noen beat-frekvens. Beats mellom to toner kan bli oppfattet av øret opp til en forskjell i frekvens på omtrent 15 Hz (Resnick 1992: 456). Når forskjellen blir større enn dette hører vi hver tone for seg, i et dissonerende eller konsorende intervall.
Analog/digital
En vanlig lydbølge er kontinuerlig både i tid og amplitude. Vi sier da at signalet er analogt, at det er definert i alle punkter og at oppløsningen er uendelig. Et digitalt signal registreres derimot som en lang streng av binære tall, enten med verdien 1 (på) eller 0 (av). Et digitalt signal er tids- og amplitudediskret, det er kun definert i de målte verdiene, og vi vet ingenting om forløpet mellom punktene.
Hvis vi ser på et mikrointervall av en lyd, kan vi definere en spesifikk nivåverdi for utslaget, et tall som definerer hvor tonen befinner seg i forhold til et nullnivå. Vi sier da at vi har registrert et sample. Når vi flytter oss til det neste mikrointervallet får vi en ny verdi, og slik kan vi fortsette bortover en lyd. Nøyaktig det samme skjer i en digitaliseringsprosess. Da er det gjerne en analog-digital (A/D) omformer som gjør målingene og lagrer dem i for eksempel en datamaskin.
Hvor små intervallene mellom hver måling er bestemmes av samplingsfrekvensen. Dette er et tall som forteller hvor mange samplinger som blir gjort per sekund. Regelen når man arbeider med digitalisering av lyd er at samplingsfrekvensen må være mer enn dobbelt så høy som den største frekvensen i stykket man tar opp (Hammer 1997:18). Halvparten av samplingsfrekvensen kalles for Nyquist-frekvensen og hvis lydsignalet overstiger denne verdien kan man enten risikere at signalet ikke registreres i det hele tatt, fordi det faller i et udefinert område, eller at det foldes nedover og simulerer falske frekvenser. Når vi vet at mennesket kan høre verdier opp til 16-20 kHz (avhengig av alder), bør samplingsfrekvensen være det dobbelte av dette hvis vi skal ta opp lyd i hele det hørbare spekteret. Det er nok derfor samplingsfrekvensen på CD-plater er satt til 44,1 kHz.
Like viktig som å bestemme samplingsfrekvensen er det å definere hvor stor oppløsningen skal være. Det vil si hvor mange forskjellige verdier man kan velge mellom når man skal beskrive utslaget. I dag er det vanlig å bruke en oppløsning på 16 bit som tilsvarer 2^16^ = 65536 punkter. Selv om dette virker som en stor verdi, viser det seg allikevel at nyansene i musikken begrenses. Mange nyere profesjonelle konvertere kommer i dag med oppløsninger på opptil 24 bit.
Når det digitale signalet skal spilles av er det viktig at avspillingsfrekvensen er den samme som samplingsfrekvensen, ellers vil man oppleve en endring i tonehøyde. Når dette er sjekket, sendes den binære tallrekken gjennom en digital-analog (D/A) omformer som skaper spenninger tilsvarende de lagrete verdiene. Deretter sendes signalet gjennom et skarpt lavpassfilter som kutter frekvenser over Nyquist-frekvensen. Til slutt forsterkes signalet slik at man kan høre lyden.
Fourieromvending
Et av de mest sentrale hjelpemidlene i digital lydbehandling kalles Fouriertransformasjon, etter den franske matmatikeren og fysikeren Jean-Baptiste Joseph Fourier. Han oppdaget at det er en likhet mellom en funksjon av en frekvens og summasjon av funksjoner av tiden t. Matematisk er dette gitt ved
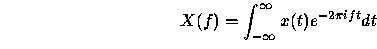
og tilsvarende blir
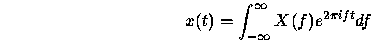
når x(t) er en funksjon av tiden t og X(F) er en funksjon av frekvensen f. Fra likningene (2) og (3) ser vi at det eneste som skiller transformasjonen og dens inverse er indeksen til e. Det er derfor enkelt å benytte transformasjonen til å regne både til og fra delfrekvensense (Moore, 1990:62).
Men disse formlene tar utgangspunkt i en lineær kurve og integrerer fra minus uendelig til pluss uendelig. Et digitalt signal er kun et endelig antall definerte punkter. Når man skal omvende et diskret digitalt signal brukes isteden DFT, den diskrete Fourier transformasjonen. Denne formelen tar utgangspunkt i samplinger av det underliggende, kontinuerlige spekteret av den underliggende, kontinuerlige bølgeformen (Moore 1990:64-65). Etterhvert har det også blitt utviklet en FFT (Fast Fourier Transform) som bruker en logaritmisk funksjon istedenfor en kvadratisk funksjon for å løse summasjonen (ib. 81-82). Særlig på større beregninger er denne svært tidsbesparende, og derfor er det denne metoden som i all hovedsak benyttes idag.
Men hva er det egentlig som skjer når man gjør en slik omforming. Jo, ved å bruke en datamaskin til å kjøre Fouriertransformasjon på en lydbølge får man et diagram hvor deltonenes amplituder vises som funksjon av frekvensen. Lyden er da vist som et spektrogram i frekvensdomenet (Hammer 1997:23). Eller som det blir sagt: “The Fourier transform … is used in many fields of science as a mathematical or physical tool to alter a problem into one that can be more easily solved” (Hoffman, u.å.). På samme måte kan man reversere prosessen og bygge opp en tone ved å addere heltallsmultipler av grunntonefrekvensen. I utgangspunktet kan man da sette opp en matematisk formel for en hvilken som helst tone for deretter å lage en perfekt reproduksjon av klangen.
Fysisk analyse av pianolyd
Det er fint å forstå teorien bak lyd og akustikk, men jeg ønsket å teste ut hvordan det hele utarter seg i praksis. Jeg laget derfor et lite forsøk for å undersøke lyd fra forskjellige pianoer.
Opptak av pianolyd
Til de digitale opptakene brukte jeg en Tascam DAT-spiller og to Neuman KM 100 kondensatormikrofoner. Mikrofonene stod på stativer i 1,5 meters høyde, omtrent to meter fra instrumentet, og med en innbyrdes avstand på 20 cm. De var rettet mot høyre og venstre kant i forhold til instrumentet for å simulere posisjonen til menneskets ører. Opptakene ble gjort i 16 bits stereo og med en samplingsfrekvens på 44,1 kHz. I bildene under har jeg mikset de to kanalene sammen for at det skal være mer oversiktlig å se signalet.

Figure 3: Roland RD-600
De akustiske opptakene ble gjort på et Yamaha og et Steinway flygel. Desverre var Steinway flygelet relativt ustemt både i forhold til seg selv og til de andre instrumentene. Opptak av digitalpiano gjorde jeg gjennom den konstante linje-utgangen på et Roland RD-600 (figur 3). Her benyttet jeg hovedinstrumentet A11 uten effekter, chorus eller reverb på lyden. På alle instrumentene spilte jeg alle C’er fra 1C til c5, ved å slå an tonen og la den klinge helt ut. Tonene kan høres i spor 1-24. I tillegg tok jeg opp tonen c1 med sustain-pedalen nede (spor 25-27).

Figure 4: En pianotone. Til venstre vises hele tonen, mens det til høyre er zoomet inn på attack og decay.
En pianotone
De fleste vet hvordan et piano høres ut, og klarer å gjenkjenne denne lyden blant mange andre lyder. Lyden fremkommer ved at en tangent trykkes ned slik at bakenden av tangenten vipper opp og slår på en hammer, som til slutt treffer selve strengen. I tillegg heves dempeputen på den aktuelle strengen, slik at tonen kan klinge fritt. Tidsforløpet av en pianotone er vist i figur 4). Til venstre er det et bilde av hele tonen, mens det til høyre er zoomet inn på attack og decay. Vi ser at attack-delen av tonen er svært kort slik at maksutslaget av lyden inntreffer nesten umiddelbart. Deretter følger en rask decay som ser tilnærmet eksponensiell ut. Så følger den betydelig lengre sustain-delen hvor tonen langsomt dør ut.
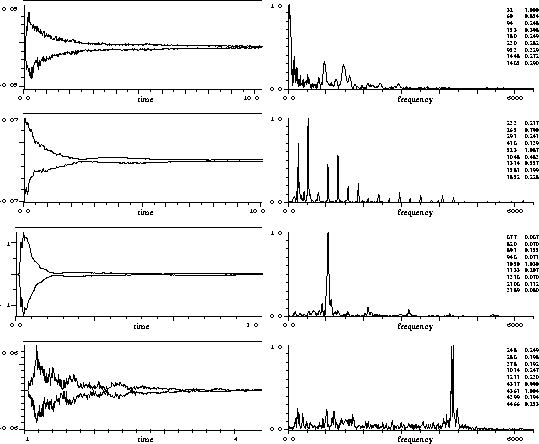
Figure 5: Fra toppen tonene 1C, c1, c3 og c5 fra Yamaha flygel
Tonene fra 1C til c5
I figur 5 ser vi tonene 1C, c1, c3 og c5 som er laget ved hjelp av programmet SND. Grafene til venstre viser lydstyrken varierende med tiden. Tidsaksen er justert for hver lyd slik at vi får med omtrent halvparten av hver av tonene. Det er interessant å legge merke til at tonene med lave frekvenser varer lenger enn tonene med høy frekvens. Tonen 1C varer omtrent 25 sekunder, c1 omtrent 15 sekunder, c3 omtrent 10 sekunder og c5 i underkant av 4 sekunder. I det nederste bildet kan det se ut som c5 har en mye mer ujevn kurve enn c3. Dette er kun fordi det er zoomet mer inn på c5.
Noe som er interessant å legge merke til er hvordan sustain-delen av tonene ser ut til å “pulsere”. Dette gjelder også for tonen 1C, selv om det i figur 5 er mest synlig i tidsspektrene til tonene c1 og c3. I tonen c3 er det en innsnevring i lydstyrken ved omtrent ved 0,5 sekunder, deretter øker lydstyrken igjen og synker til en ny minimumsverdi ved 1,7 sekunder. Denne effekten skyldes beats og interferens mellom de forskjellige strengene. En slik pulsering er vanlig og en av de vanskeligste delene å simulere ordentlig på et digitalt piano.
Bildene til høyre i figur 5 viser frekvensspekteret for hver av de fire tonene. Her er det brukt en Fourier-omvending på det første punktet i tidsspekteret, med en vindusbredde på 4096 punkter. For hver tone kan vi se at det er en eller flere topper som markant skiller seg ut. Dette er da etter all sansynlighet grunntonen eller en av dens nærliggende. Verdiene til frekvens og relativ amplitude for de største toppene står i tallkolonnene helt til høyre. Alle disse verdiene er beregnet i begynnelsen av attacket og kan derfor være noe upresise for å angi den generelle grunntonefrekvensen for tonen. De viser imidlertid at 1C har grunntone nær 32 Hz, c1 nær 265 Hz, c3 nær 1050 Hz og c5 nær 4361 Hz. Tonen c1 skal egentlig være på omtrent 261 Hz, så de beregnete verdiene stemmer ganske bra. En kontrollregning viser også at en dobling i frekvens gir en stigning på en oktav.

Figure 6: Tonen c1 i tidsspekter. Øverst Roland RD-600 A11, i midten Steinway & Sons flygel og nederst Yamaha flygel
Tonen c1
Figur 6 viser et forstørret tidsspekter for tonen c1 fra henholdsvis Roland, Yamaha og Steinway. Her kan vi se bølgeformen i tidsrommet fra 0 til 0,03 sekunder akkurat i attack-fasen. Det er interessant å legge merke til hvor forskjellige bølgene ser ut, selv om de høres relativt like ut når de spilles av etter hverandre (spor 29). Dette skyldes at de er bygget opp av forskjellige sinufunksjoner. Faseforskjell mellom de forskjellige delbølgene kan være grunnen til at lydene ser svært forskjellige ut, men lyder ganske likt. Legg merke til hvor harmonisk Steinway-tonen ser ut i forhold til de andre. Dette passer med at denne tonen høres litt mykere ut i klangen.
Lydsyntese
På grunn av en enorm utvikling innen maskinvare og datamaskiner de siste årene, har det også blitt brukt en mengde forskjellige metoder for å syntesere, eller kunstig skape lyd. Felles for alle er at man er avhengig av en oscillator som kan generere de forskjellige funksjonene som angis, og at man har en forsterker som varierer amplituden på signalet. I tillegg er det vanlig å bruke forskjellige former for envelope for å forme hver tone slik man ønsker. Jeg skal her presentere noen av de mest sentrale teknikkene som har vært i bruk de siste årene.
Additiv syntese
Additiv syntese går ut på at man adderer sinusfunksjoner for å skape en tone. Vanligvis gjøres dette ved å gi verdiene til de forskjellige frekvenstoppene man ønsker og de respektive amplitudeverdiene. Deretter anvendes en av metodene for Fourieromvending og man får den sammensatte lyden. Hvis man er nøyaktig med å angi frekvenser kan man på denne måten produsere svært avanserte lyder. Problemet er gjerne at denne metoden medfører mange beregninger. Det har derfor vært vanlig å bruke den inverse av FFT (Fast Fourier Transform), som utfører beregningene mye raskere enn vanlig Fouriertransformasjon (Hammer 1997:49).
Subtraktiv syntese
Istedenfor å legge til funksjoner, tar man utgangspunkt i en lyd som er rik på overtoner og subtraherer deretter deler av lyden. Som startbølger kan man bruke sinus, firkant, sagtann, pulstog eller samplede lyder. En sagtann-bølge inneholder alle de harmoniske overtonene, med en gradvis senking av amplituden for hver av de harmoniske. En firkantbølge er bygget opp av kun de oddeharmoniske overtonene, mens pulsbølgen består av alle de harmoniske overtonene med samme amplitude. Hele poenget er at man sender et slikt signal gjennom et filter og så kommer en lyd ut. Det er vanlig å bruke lavpassfiltere som kutter bort frekvenser over en viss verdi. Ved å endre på cut-off frekvensen på filteret kan forskjellige lyder synteseres. Dette var en populær metode i mange av de tidlige synthesizerne, fordi den ikke krever mer enn noen få oscillatorer og filtre for å lage mange forskjellige lyder (Svinndal 1992:8-11).
FM-syntese
FM-syntesen har vært svært mye brukt i synthesizere og lydkort til datamaskiner. Den går i all hovedsak ut på at man bruker en oscillator til å sette opp en bærebølge (carrier). Deretter benyttes en lavfrekvent oscillator (LFO), som kalles modulator, for å styre frekvensen til bærebølgen. Klangfarven til tonen avhenger av forholdet mellom de to frekvensene, og kalles modulasjonsindeksen. Vanligvis brukes det flere oscillatorer for å endre lyden. En envelope på modulator endrer klangfarven, mens envelope på carrier endrer dynamikk i styrken. Ved å kombinere disse kan man lage en generell operator som kan inngå i en algoritme (Hammer 1997:50). Denne metoden ble svært populær, og blant annet Yamaha utviklet en serie med synthesizere som brukte denne teknikken. Metoden har imidlertid sine begrensninger og brukes nesten ikke lenger idag:
“In playback of music, synthesis allows for creation of many different sounds which are not otherwise available. … But FM synthesis is only one method of generating sounds, and is not a particularly realistic method. In fact, though developed for professional musical instruments, FM synthesis is largely obsolete in that market today” (White 1996).
Sampling
Sampling er ikke egentlig en “ren synteseform”. En sampler gjør et opptak av en lyd og kan deretter spille den av igjen. Dette gir i utgangspunktet en identisk tone når man spiller den av. Når man ønsker å variere tonehøyden endres avspillingshastigheten til den aktuelle lyden. Tilsvarende brukes en forsterker for å variere lydstyrken. Det er denne metoden som i all hovedsak brukes i lydkort og digitalpianoer i dag, gjerne sammen med noen av de andre syntesemodellene. Men det er ikke gitt at resultatet blir bra ved å bruke samplinger for å lage lyder, noe jeg kommer tilbake til i neste kapittel.
Fysisk modellering
De siste årene har fysikerne begynt å forstå hvilken funksjon og innvirkning hvert enkelt element i et instrument og dets omgivelser har for den endelige lyden. Når hver liten detalj som for eksempel hammerens slag på strengen, interferens mellom strengene og resonans i kassen kan beskrives fysisk, skulle det være mulig å modellere en tone. I tillegg vil et instrument basert på fysisk modellering kunne reagere realistisk på forskjellige spilleteknikker, for eksempel variasjon i anslag på tangenten. Dette krever naturlig nok svært mange beregninger, og man kan ende opp med å måtte løse likninger med tusenvis av ukjente. Med utviklingen av kraftige datamaskiner og stabile programmer er dette mulig, selv om det kan ta lang tid.
Modalys er et dataprogram basert på fysisk modellering. Her opererer man i et grafisk brukergrensesnitt hvor man enkelt kan plassere forskjellige elementer i et virtuelt rom på skjermen. Valgmulighetene spenner over alt fra strenger, en resonanskasse og hammere som slår, til å definere flere strenger som klinger med og pedalbruk. Til slutt kan man velge hva slags rom instrumentet befinner seg i før man ber maskinen regne ut lyden. I utgangspunktet virker det svært enkelt å lage en god lyd, men det kreves mye erfaring før man får et tilfredsstillende resultat.
Denne typen modellering er selvfølgelig også avhengig av hvordan de forskjellige elementene er beskrevet matematisk. Det er vanlig å ta utgangspunkt i fysiske målinger av et instrument, og da minsker fleksibiliteten betraktelig. Foreløpig er dette en relativt ny metode, så det utvikles stadig nye pakker med beskrivelser av instrumenter eller instrumentdeler.
En slik beskrivelse er Karplus-Strong-algoritmen. Dette er egentlig et filter laget for å syntesere lyden av klimpring på en streng. La oss tenke oss at vi sitter på et bestemt sted på en streng og observerer hvordan denne beveger seg i dette punktet. Når strengen slås an spres lydbølgene i begge retninger vekk fra dette punktet. Bølgene treffer hver sin ende av strengen og reflekteres tilbake. Hele tiden foregår det imidlertid en dempning av signalet på grunn av friksjon mellom streng og luft og de fastspente punktene. Strengen fungerer altså i seg selv som et lavpassfilter, som begynner med å fjerne de høyeste frekvenskomponentene. I tillegg opplever vi en interferens når bølgene fra hver side “treffer” hverandre. Bølgene beveger seg frem og tilbake på strengen og interfereres og filtreres mer for hver gang, helt til lyden dør helt ut.
Pluck er en Karplus-Strong algoritme som gir en svært realistisk lyd (spor 31). Den er også et godt utgangspunkt for syntese av mange forskjellige lyder (Hammer 1997:59-60).
Forsøk på syntese av pianolyd
Jeg ønsket å teste om jeg kunne klare å syntesere en pianotone helt fra grunnen av ved å bruke forskjellige synteseprinsipper. Som verktøy benyttet jeg lydsynteseprogrammet Csound. Programmet fungerer som en kompilator som leser en orkesterfil og en partiturfil og lager en lydfil på bakgrunn av de oppgitte verdiene.
Jeg bestemte meg for å lage pianotoen c1. Første punkt var da å finne ut hvilken grunntonefrekvens denne tonen har. Dette kan jeg beregne ved å se på forholdstallet mellom c1 og a1 som er 3:5. Når a1 har frekvens 440 Hz, gir dette at c1 er 264 Hz. Jeg ønsket å se på frekvensspekteret fra en av pianotonene jeg hadde tatt opp, så jeg brukte programmet SND for å Fourieromvende pianotonen c1. Verdiene jeg fikk var som i tabell 1. Her er grunntonen på 261 Hz, så jeg valgte å bruke denne verdien istedenfor min beregnete frekvens.
Tabell 1: Frekvens og relativ amplitude for pianotone c1
| Frekvens (Hz) | Relativ amplitude |
|---|---|
| 261 | 1.000 |
| 523 | 0.387 |
| 786 | 0.212 |
| 1048 | 0.344 |
| 1313 | 0.183 |
| 1846 | 0.155 |
| 2386 | 0.0975 |
Jeg begynte med å lage en ren sinustone med frekvens 261 Hz. Tonen er angitt som instrument 1 i orkester-filen til Csound (figur 8). Fra koden ser vi at det brukes en oscillator for å lage en tone med amplitude 10 000 (maks 20 000), frekvens 261 Hz og bølgeform nummer 1. I partiturfilen (figur 7) angis det at tonen skal spilles i 4 sekunder. Lyden vi får (spor 30) er altså en helt ren sinustone med frekvens 261 Hz.
Istedenfor å direkte addere de andre harmoniske til tonen, forsøkte jeg å bruke en sidefunksjon til Csound som kalles hetro (Hetrodyne filter analysis). Denne algoritmen leser en lydfil og skriver de harmoniske til en fil. Filen leste jeg inn i instrument 2 i orkester-filen (figur 8), og instrumentet ble spilt av. Dette hadde ingen særlig effekt, så jeg bestemte meg for å forsøke å addere delkomponenter isteden.
De forskjellige frekvensene og de relative amplitudene hadde jeg allerede (tabell 1). Disse ble skrevet inn som kall på hver sin oscillator i instrument 3 (a1-a7). Hver oscillator tar parametrene frekvens, amplitude og kurveform. De forskjellige funksjonene adderes i a8, og nå er selve tonen skapt. For å legge på en envelope som endrer amplituden over tid, kalles det i a9 på funksjonen expseg. Den legger en eksponensiell decay på lyden, og tar parametrene startverdi, varighet av første segment og verdi etter første segment. Decayen adderes til den sammensatte bølgen i a10. Nå begynner lyden å minne litt om en pianotone.
Jeg hadde lyst til å teste ut hvordan Karplus-Strong algoritmen pluck klarer å simulere strenganslag. Denne er lagt til i a11 og adderes til de andre verdiene i a12. Kommandoen garev hopper vi over foreløpig og ser at dermed er dette instrumentet ferdig definert.
For å forsterke anslaget av tangenten idet den treffer strengen, la jeg til en ny pluck i instrument 4. Denne har en mye større amplitude enn den forrige, slik at den høres tydeligere. Kommandoen linen gir en skarp lineær økning i verdi og en rask decay. Dette instrumentet kalles i partiturfilen rett før selve tonen for å simulere et hardt strenganslag.
For å skape en ordentlig konsertstemning la jeg til slutt på litt romklang. Denne er definert i instrument 99 og kalles ved tid=0 i partiturfilen slik at den blir global og gjelder for alle instrumenter som spilles av. Det er boksen reverb som lager klangen med den globale variabelen garev som paramater. Vi så i instrument 3 at garev der fikk verdiene fra den sammensatte tonen.
I partiturfilen settes selve lyden til å komme 0.03 sekunder etter strenganslaget. Dette gjorde jeg for å simulere en ørliten forsinkelse i attack. Til slutt kjøres de to filene gjennom Csound-kompilatoren, og lyden blir som i spor 32. Med litt godvilje kan man jo gå med på at tonen unektelig har noe av den samme klangen som en ekte pianotone. Selv synes jeg strenganslaget ble for skarpt, men dette skyldes at pluck egentlig er skrevet for å simulere klimpring på en gitarstreng. Forsinkelsen jeg satte inn på tonen virker litt for lang. Decay og sustain mangler også den riktige kurven før man kan overbevises om at det er et ordentlig piano vi har å høre med.
Selv om lyden kanskje ikke ble så overbevisende, fikk jeg ihvertfall sett og testet ut hvordan man synteserer en tone og bruker noen av verktøyene som kan endre lyden.
f1 0 4096 10 1
;instrument Start Varighet
; i1 0 4
; i2 0 4
i3 0.03 8 ; Lyd
i4 0 1 ; Strenganslag
i99 0 9 ; Klang i 5 sek.
e
Figur 7: Csound score-fil for enstrøken c
sr = 44100 ; Samplerate
kr = 4410 ; Kontrollrate
ksmps = 10 ; Forskjell sr/kr
nchnls = 1 ; Antall kanaler
garev init 0 ; Initialisering av garev
instr 1 ; Enkelttone 261 Hz
a1 oscil 10000,261,1
out a1
endin
instr 2 ; Resampling fra hetro-fil
a1 adsyn 1,1,1,"4c1.hetro"
out a1
endin
instr 3
a1 oscil 10000,261,1 ; Grunntone med frekvens 261 Hz
a2 oscil 3870,523,1
a3 oscil 2120,786,1
a4 oscil 3440,1048,1
a5 oscil 1830,1313,1
a6 oscil 1550,1846,1
a7 oscil 975,2386,1
a8 = a1+a2+a3+a4+a5+a6+a7 ; Sammenlegging av forskjellige toner
a9 expseg 1,1,.3 ; Eksponensiell decay
a10 = a8*a9
a11 pluck 200,261,261,0,1 ; Attack med Karplus-strong
a12=a10+a11
garev = garev+a12 ; Initialisering til romklang
out a12
endin
instr 4 ; Strenganslag med Karplus-Strong
a1 pluck 2000,261,261,0,1
a2 linen a1,.1,p3,p3*.3
out a2
endin
instr 99 ; Romklang
asig reverb garev*.1,2 ; 2 sekunders klang
out asig
garev = 0
endin
Figur 8: Csound orkester-fil for enstrøken c
Digitalt piano
Dagens digitale pianoer benytter seg i all hovedsak av samplingsteknikken. Som tidligere beskrevet, spiller man da av en digitalisert pianolyd. Oscillatorer varierer frekvensen, og en forsterker styrer lydstyrken. Dette virker relativt greit, men det er en rekke forskjellige punkter som kompliserer prosessen.
Først og fremst teller klangfarven inn. En lys og en mørk tone har en helt forskjellig oppbygning så hvis vi spiller av tonen 1C med hastighet som en c5 så høres det relativt spinkelt ut (spor 33). Når tonen c5 spilles av med hastighet som 1C får man definitivt ikke pianofølelse (Legg merke til at venstre kanal spiller lyden tidligere enn høyre kanal, sannsynligvis fordi den opprinnelige lyden først ble fanget opp av venstre mikrofon. Den ekstreme hastigheten lyden spilles av på audioaliserer denne effekten.) (spor 34). For å løse dette problemet kan man tenke seg at det vil være best å ta opp hver eneste pianotone for seg. Dette er nok best, men det ville krevet stor lagringsplass om man skulle ha liggende 88 forskjellige lyder som hele tiden skal være klar til å spilles av. Løsningen til nå har derfor vært at man definerer 5-6 soner på klaviaturet som har hver sin lyd. Det er gjerne en lyd som dekker nesten alle tonene fra 1C til c1, mens resten av tonene fordeles på de lyse intervallene. Dette er fordi klangfarven endres betydelig mer i de lyse partiene. På denne måten sikres man en naturlig tone samtidig som størrelsen på lydfilene holdes nede.
Jeg ønsket å teste ut dette på egenhånd og forsøkte derfor å lage mitt eget samplepiano. Jeg brukte programmene SampleCell og ProTools for å sette opp et instrument. Der importerte jeg en pianodefinisjon, og la så inn lyder fra Steinway-flygelet som dekket tonene fra 1C - c5. Jeg lot tonene være definert over en oktav, slik at lyden fra tonen c1 ble brukt på alle notene mellom giss og g1. Når man hører på en skalaoppgang av dette instrumentet (spor 35) kan man tydelig høre overgangen fra en lyd til en annen. Dette kan løses ved at man innfører en funksjon som mikser to lyder i overgangsområdene. En annen mulighet er å normalisere tonene og modifisere hver av dem slik at de bedre “passer inn” i hverandre.
Men på samme måte som klangfarven er forskjellig for mørke og lyse toner, varierer den også for sterke og svake enkelttoner. Hvis man bare demper en sterk lyd vil det ikke høres særlig naturlig ut. Derfor er det vanlig at man har tre forskjellige lyder liggende per tone. Disse må også behandles slik at overgangsområdene høres naturlig ut. Et slikt instrument vil altså bestå av tre ganger fem forskjellige lyder. Hvert sample er i stereo og varer i omtrent fire sekunder. Når vi vet at det går omtrent seks sekunder stereolyd per megabyte, så trengs det en lagringsplass på omtrent ti megabyte bare for ett instrument. Vanlige digitalpianoer har gjerne mellom 10 og 100 forskjellige instrumenter liggende lagret. Dette er mulig ved hjelp av kraftig kompresjon av lydfilene og streng seleksjon av de viktigste områdene i hver lyd. Desverre medfører dette en betraktelig senkning av lydkvaliteten.
Vi har sett at å bruke en envelope for å forme lyden er en effektiv metode. En samplet lyd trenger egentlig ikke så mye korreksjon i attack og decay områdene. Det er gjerne sustain-delen som er problemet. Som vi så fra analysen av en tone, så “pulserer” lyden i sustain-området, og hvis vi skal få en realistisk lyd er det viktig at dette kommer med. Dette gjøres ofte ved å loope et spesielt segment i lyden, men dette er en vanskelig sak. I mange digitalpianoer kan man høre at det hakker i loopingen og dette er svært uheldig.
Men det er en mengde lyder i et akustisk instrument som ikke nødvendigvis kommer fra en spesiell tone. En av disse er støy fra bevegelse av tangent og hammer. I et stort lydbilde er ikke dette særlig påfallende, men det kan være med på å endre klangfarven noe. En annen detalj er lyden fra fingeren som treffer tangenten. Dette kan være viktig å tenke på hvis man skal lage lyden slik den høres ut for pianisten.
Det jeg tror er den vanskeligste delen å simulere, er bruken av pedaler. Dempepedalen kan forholdsvis enkelt justeres, men sustain-pedalen volder større problemer. Når denne pedalen trykkes ned, løftes dempeputene på alle strengene slik at de kan klinge med. Nå er det slik at hvis tonen c1 spilles så vil også alle strenger som er med i overtonerekken til c1 begynne å vibrere. Selv om disse signalene er svake vil de på sin side sette i bevegelse tonene i sine overtonerekker, osv. Alle disse forskjellige lydbølgene beveger seg frem og tilbake i instrumentet og interferer konstruktivt og destruktivt med hverandre samt stadig flere strenger. Når pedalen ligger over lengre tid og man i tillegg spiller flere toner på en gang og etter hverandre, blir lydbildet til slutt ekstremt komplisert. På sporene 25-27 har jeg gjort opptak av tonen c1 med pedalen liggende nede før anslaget. Mens de akustiske instrumentene tydelig får en mer “utflytende karakter” endres ikke lyden på digitalpianoet nevneverdig.
Alt i alt ser vi at det er en rekke forskjellige faktorer å ta hensyn til hvis vi ønsker å lage et digitalt piano. Og enda har vi ikke begynt å se på avspillingsmedium. Generelt så begrenses utviklingen av gode lyder på grunn av lagringskapasitet. Men det hjelper ikke bare å kunne ta opp flere lengre og bedre lyder. Forståelsen av hvordan tonene fungerer sammen og i forhold til instrumentkassen er vel så viktig. Fremtiden er kanskje en form for kombinasjon av sampling og fysisk modellering. Da vil man kunne få et instrument med “ekte” lyd som oppfører seg som et ordentlig piano.
Blindtest
For virkelig å teste ut om folk klarer å høre forskjell på et digitalt eller akustisk piano, laget jeg en liten blindtest.
Gjennomføring av testen
Jeg valgte å operere med to små lydsnutter, en klassisk og en jazz/blues. Hvert av disse sporene tok jeg opp på seks forskjellige instrumenter, tre vanlige og tre digitale. Da opptakene ble utført hadde jeg desverre ikke tilgang til noe ordentlig flygel. Jeg brukte isteden tre pianoer fra henholdsvis Yamaha, schimmel og Grotwig-Steiman. De digitale instrumentene ble valgt fra Roland RD-600. Opptakene ble gjort med Tascam DAT-spiller og to Neuman MK 100 kondensatormikrofoner. Avspillingsmediet var en Sony MD-R50 med Sennheiser hodetelefoner. Testpersonene ble forklart at de skulle angi om de syntes instrumentet virket akustisk eller digitalt. Jeg forklarte at snuttene var tatt opp i forskjellige rom, med forskjellige instrumenter og at det ikke nødvendigvis behøvde å være halvparten digitalt eller akustisk. I tillegg opplyste jeg om at noen av de digitale instrumentene kunne være stemt litt opp eller ned. Sporene ble spilt av slik de er på CDen (spor 36-37). Når det var ønskelig stoppet jeg avspillingen eller repeterte en snutt.
Tabell 2: Resultater blindtest. Prosentene viser hvor mange som trodde at lyden var digital eller akustisk.
| Snutt nr | Digital | Akustisk | Instrument |
|---|---|---|---|
| 1 | 75% | 25% | Roland RD-600 A11 |
| 2 | 42% | 58% | Yamaha piano |
| 3 | 50% | 50% | Schimmel piano |
| 4 | 58% | 42% | Roland RD-600 B13 u/reverb 438 Hz |
| 5 | 17% | 83% | Grotwig-steiman |
| 6 | 83% | 17% | Roland RD-600 A21 u/reverb 442 Hz |
| 1 | 50% | 50% | Schimmel piano |
| 2 | 92% | 8% | Roland RD-600 A11 |
| 3 | 75% | 25% | Roland RD-600 A21 u/rev 442 Hz |
| 4 | 8% | 92% | Yamaha piano |
| 5 | 58% | 42% | Roland RD-600 B13 u/rev 438 Hz |
| 6 | 42% | 58% | Grotwig-steiman |
Resultater
Resultatene (tabell 3) viser at det var relativt stor usikkerhet om de forskjellige sporene. Totalt gjennomførte 12 mennesker testen. Åtte av disse var musikere eller musikkstudenter og av disse spilte fire piano. Generelt hadde disse færre feil enn de andre testepersonene. Fire av personene hadde kun to feil, mens resten bommet på flere. Ingen traff riktig på alle!
Generelt ser det ut til at Schimmel-pianoet voldte meste problemer, ettersom det både på klassisk og blues var halvparten som trodde det var et digitalt piano. Roland RD-600 B13 var også relativt likt representert. Den digitalpianolyden som jeg liker best selv og som også er definert som hovedlyd, Roland RD-600 A11, ble ganske tydelig gjenkjent som digitalpiano. Dette kan kanskje skyldes at det var brukt reverb gjennom pianoet under opptaket. Interessant var det ihvertfall at mange uttrykte frustrasjon over at de syntes det var vanskelig å høre forskjell de forskjellige instrumentene. De fleste var også overasket over kvaliteten på digitalpianoene.
Usikkerhetsmomenter
Det er selvfølgelig en hel mengde med usikkerhetsmomenter. Først og fremst ble ikke opptakene av de akustiske instrumentene like bra som jeg hadde håpet. Jeg hadde store problemer med overstyring og klipping på DAT-spilleren og ved å senke nivået ble lyden relativt mye svakere enn de på de digitale instrumentene.
For de andre blir det lett opptakstekniske ujevnheter når ikke instrumentene står i samme rom og mikrofonene plasseres litt forskjellig. På det digitale pianoet brukte jeg linjeutgangen, fordi dette burde generere en mest mulig naturlig tone i henhold til klangidealene produsentene arbeider med. Ideelle opptak måtte ha blitt tatt i ett rom hvor mikrofonene stod konstant og instrumentene ble flyttet frem og tilbake, for å sikre jevne akustiske forhold.
Avspillignsmediet var en Sony MZ-R50 minidisc-spiller. Denne ble benyttet istedenfor DAT-spiller på grunn av en mer hendig størrelse. Problemet med minidisc-formatet er at det er komprimert, fra omtrent 750 MB til 160 MB for 74 minutter stereo, ved at det kuttes i den øverste og nederste delen av spekteret. Dette skaper selvfølgelig en viss reduksjon i noen overtoner, selv om man skal være særlig trenet for å legge merke til dette. Det mest ideelle hadde selvfølgelig vært å sitte i et lydrom og spille av opptakene med gode høyttalere. Jeg ønsket imidlertid å teste mange “normale” mennesker og stilte meg derfor opp på Frederikkeplassen med et par kraftige hodetelefoner. Her er det endel bakgrunnsstøy og testpersonenene fikk heller ikke særlig lang tid til å lytte på de forskjellige opptakene. Meningen var heller ikke en grundig analyse, men bare at testpersonene skulle beskrive den umiddelbare følelsen av instrumentet.
Uansett viser hovedtrenden at flertallet fremdeles klarer å høre forskjell på et akustisk og et digitalt instrument selv om noen av instrumentene lå nærme halvparten. Dette er imidlertid mye bedre enn hvis man hadde gjort en lignende test for noen få år siden.
Konklusjon
Som vi har sett er pianoet et instrument med sammensatt og kompleks lyd. Selv om man nå begynner å utvikle teknikker som gjør at man får svært realistisk pianolyd, så er det fremdeles mange små uavhengigheter som gjør at det vanskelig å skapet et troverdig piano.
Min blindtest på forskjellige mennesker viste jo at de fleste også hadde problemer med å skille noen av instrumentene.
Har det så noen hensikt å forsøke å lage et digitalt instrument? Det kan jo aldri helt bli det samme som et ekte instrument. Jeg tror det er svært viktig å arbeide med å skape et perfekt digitalt instrument. Gjennom arbeidet vil man jo forstå veldig mye av hvordan man kan forbedre et ekte piano, og i tillegg så kan man utvikle svært gode digitale instrumenter som kan brukes til for eksempel MIDI eller konsertanledninger hvor signalet allikevel skal forsterkes. På sikt vil kanskje instrumentene bestå av an blanding av akustiske egenskaper og digitale fortrinn. Fremtiden er spennende!
Bibliografi
- Bateman, Wayne A. (1980): Introduction to Computer Music, John Wiley & Sons, New York
- Benestad, Finn (1985): Musikklære, TANO, Oslo
- Hammer, Øyvind (1997): Digital lydbehandling, NOTAM, Oslo
- Hoffman, Forrest (u.å.): An Introduction to Fourier Theory, http://aurora.phys.utk.edu/ forrest/papers/fourier/index.html, University of Tennessee, Knoxville
- Proakis, John G. og Manolakis, Dimitris G. (1992): Digital Signal Processing. Principles, Algorithms, and Applications, Macmillan, New York
- Resnick, Robert; Halliday, David and Krane, Kenneth S. (1992):Physics, vol I, John Wiley & Sons, New York
- Moore, F. Richard (1990): Elements of Computer Music, Prentice Hall, New Jersey
- Svinndal, Anders (1992): Synthesizeren som erstatning for akustiske instrumenter, Semesteroppgave musikkvitenskap, Oslo
- Vistnes, Arnt Inge og Bugge, Lars (1993): FYS 115 øvelse 12 Digitalisering av lyd, Labintroduksjon Fysisk institutt, Oslo
- Vistnes, Arnt Inge og Bugge, Lars (1993): FYS 115 øvelse 20 Syntese av lyd og digital filtrering, Labintroduksjon Fysisk institutt, Oslo
CD-spor
Tabell 3: Spor på den vedlagte CDen
| Spor | Beskrivelse |
|---|---|
| 1 | Yamaha flygel, tonen 1C |
| 2 | Yamaha flygel, tonen C |
| 3 | Yamaha flygel, tonen c |
| 4 | Yamaha flygel, tonen c1 |
| 5 | Yamaha flygel, tonen c2 |
| 6 | Yamaha flygel, tonen c3 |
| 7 | Yamaha flygel, tonen c4 |
| 8 | Yamaha flygel, tonen c5 |
| 9 | Steinway \& Sons flygel, tonen 1C |
| 10 | Steinway \& Sons flygel, tonen C |
| 11 | Steinway \& Sons flygel, tonen c |
| 12 | Steinway \& Sons flygel, tonen c1 |
| 13 | Steinway \& Sons flygel, tonen c2 |
| 14 | Steinway \& Sons flygel, tonen c3 |
| 15 | Steinway \& Sons flygel, tonen c4 |
| 16 | Steinway \& Sons flygel, tonen c5 |
| 17 | Roland RD-600 A11, tonen 1C |
| 18 | Roland RD-600 A11, tonen C |
| 19 | Roland RD-600 A11, tonen c |
| 20 | Roland RD-600 A11, tonen c1 |
| 21 | Roland RD-600 A11, tonen c2 |
| 22 | Roland RD-600 A11, tonen c3 |
| 23 | Roland RD-600 A11, tonen c4 |
| 24 | Roland RD-600 A11, tonen c5 |
| 25 | Yamaha flygel, tonen c1 med pedal nede |
| 26 | Steinway \& Sons flygel, tonen c1 med pedal nede |
| 27 | Roland RD-600 A11, tonen c1 med pedal nede |
| 28 | Yamaha flygel tonene 2C, c1, c3, c5 |
| 29 | Tonen c1 fra Roland/Steinway/Yamaha |
| 30 | Sinustone med frekvens 261 Hz |
| 31 | Karplus-Strong Pluck algoritmen |
| 32 | Forsøk på syntese av pianolyd, tonen c1 |
| 33 | Tonen 2C spilt med frekvens som tonen c5 |
| 34 | Tonen c5 spilt med frekvens som tonen 2C |
| 35 | Forsøk på å lage et samplepiano |
| 36 | Blindtest, klassiske snutter |
| 37 | Blindtest, gospel/blues snutter |
